sm_regression

Daniel D. Sjoberg

2019-01-23

Introduction

The sm_regression() function performs kernel weighted regression. After the the model is specified (data = cancertx, method = "coxph", formula = Surv(time) ~ age), an ancillary variable is specified (weighting_var = "marker") and the model is estimated weighted on this variable.

The following examples focus on time-to-event endpoints. The example data set is simulated from a Cox regression model.

\[ h(t) = h_0(t)e^{\textbf{X}\beta} \]

with \(h_0(t) = 1\) and \(\textbf{X}\beta = 0.02 * age - 0.2 * marker\). The independent variables age and marker are independent from one another. The example data set containts the following columns:

time    Years from cancer treatment to death
age     Age at treatment
marker  Marker level at treatment
survt1  True 1 year survival probability

library(sjosmooth)
library(dplyr)
# loading data from sjosmooth github page
load(url("https://github.com/ddsjoberg/sjosmooth/blob/master/examples/cancertx.rda?raw=true"))

cancertx %>% select(time, age, marker, survt1) %>% head() %>% knitr::kable()

time	age	marker	survt1
4.396865	12.79050	10.052925	0.8411829
1.761713	32.70496	8.164047	0.6867428
4.401422	23.16842	8.725925	0.7576508
1.027328	30.00945	12.923154	0.8715716
1.979813	31.51574	9.909102	0.7719386
2.009533	38.03416	7.372298	0.6127544

The simualted data contains 10,000 observations.

Example

Kernel smoothing can be computationally intense on large data sets. The following code was run to get the example object sm_regression_ex1 and the results saved to GitHub.

library(survival)
library(sjosmooth)
sm_regression_ex1 =
  sm_regression(
    data = cancertx,
    method = "coxph",
    formula = Surv(time) ~ age,
    weighting_var = "marker",
    newdata = dplyr::data_frame(marker = seq(5, 15, 0.5))
  )

The data in the cancertx data frame was simulated from a Cox regression model with linear predictor.

\[ \textbf{X}\beta = 0.02 * age - 0.2 * marker \]

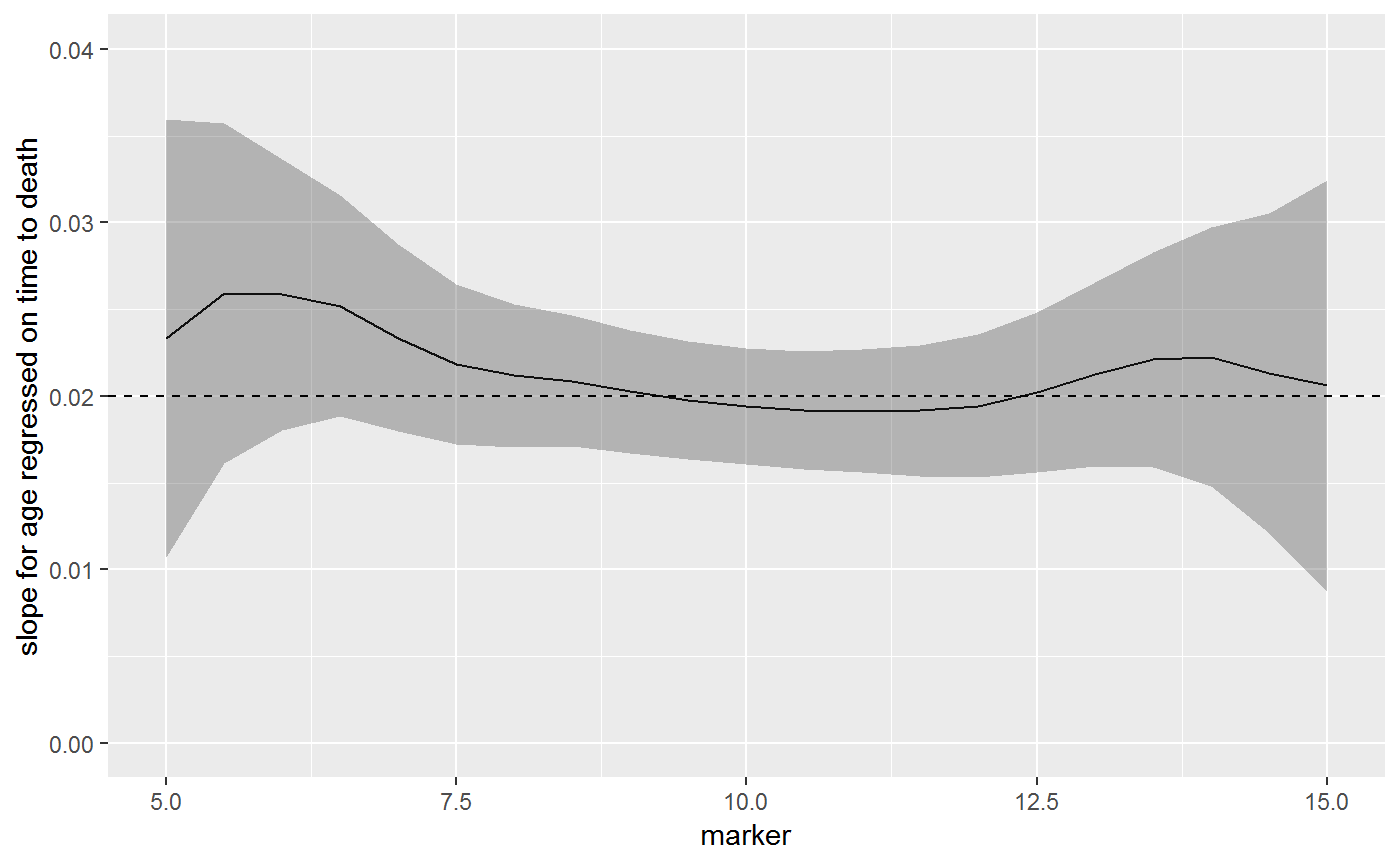
In the model age and marker level are independent, and therefore, the univariate model the slope coefficient for age remains \(\beta_{age} = 0.02\)

The beta coefficient is the same across all marker levels. In the figure below, the solid black line is the estimates beta coefficient (with 95% CI), and the dashed line is the true value.

library(ggplot2)
library(survival)
# loading example results from sjosmooth github page
load(url("https://github.com/ddsjoberg/sjosmooth/blob/master/examples/sm_regression_ex1.rda?raw=true"))

# plotting regression model coefficient by marker level
plot_data =
  sm_regression_ex1 %>%
  mutate(
    age.coef = purrr::map_dbl(model_obj, ~coef(.x)),
    age.ci = purrr::map(model_obj, ~confint(.x) %>% as_data_frame())
  ) %>%
  select(newdata, age.coef, age.ci) %>%
  tidyr::unnest(age.ci, newdata)

ggplot(plot_data, aes(x = marker, y = age.coef)) +
  geom_line() +
  geom_ribbon(aes(ymin = `2.5 %`, ymax = `97.5 %`), alpha = 0.3) +
  geom_hline(aes(yintercept = 0.02), linetype = "dashed") +
  scale_y_continuous(limits = c(0, 0.04)) +
  labs(
    y = "slope for age regressed on time to death"
  )